Cephalopodaphilia: Tech Details

Procedural generation is the creation of form, colour or movement through direct calculation. This is in contrast to the more usual route of storing and retrieving pictures, animations or 3D objects pre-generated by humans.

Proceduralism isn't a new concept - lots of contributors have embiggened the space, many in quite unique ways. Some of the names that come to mind include Benoit Mandelbrot and Edward Lorenz with their iterative fractal systems: the granddaddys of proceduralism. Ed Catmull, along with colleague Raphael Rom, designed a conveniently malleable curve or 'spline'.

More recently Ken Perlin cornered the market in 'noise': an extremely versatile procedural building block. Many of the visual effects in movies, games and TV use Perlin noise in some form or other. Concurrently with Perlin but over in the UK, David Braben and Ian Bell built a game called Elite whose universe was procedurally generated. Elite had 8 galaxies, each containing 256 planets - not bad for the time.

Bringing us up to date, modern GPUs and graphics tools exhibit procedural generation features.

We don't need all that horsepower just for a few tentacles though ;)

Preliminaries

The goal is to reproduce or at least ape some characteristics of something that exists in nature. To that end, I have tried to tie tentacular reality to these notes by including small observations to help illustrate each design decision.

We are producing images of tentacles - that means any vector algebra presented will be 2-dimensional, unless otherwise stated.

So with the background out of the way, on to the detail.

Foundations: The Curve

The backbone of this model is a realistic curve - one that has proportions and curls like real tentacles.

First though we need a way to draw a curve. A simple solution is to observe the way one might draw a curve on paper:

1. Pick a position
2. Pick a direction
3. Step away from our position in our direction
4. Repeat steps 2 and 3 until happy

p(n+1) = p(n) + (segment_length * direction)

Lets also define a termination condition: a fixed number of line segments N for our curves.

Its often easier to perform calculations along a curve with some notion of where on the curve we are. The usual solution is to define a parameter t which represents a position on the curve from 0 to 1:

t = n / (N-1)

From Curve To Tendril

There are 2 main tunable parameters in our curve model. By altering these, one can produce essentially any curvey shape.

seg_length, the line segment size, affects overall curve length. Segment size also interacts with rate of change in direction. Smaller step size produces tighter curves.

direction controls the amount of curvature introduced at each step of the curve.

Observation: tentacles tend to point in a single general direction.

We can achieve this effect by using a single curve direction over the whole curve and adding small offsets or 'perturbations' at each step:

direction = curve_direction + direction_perturbation

Observation: tentacles have tighter curvature towards the ends.

To reproduce this, we perturb our direction more towards the end of the curve:

direction_perturbation = perturb() * (1-t)

where perturb() gives some smoothly changing value thats small in comparison to the whole curve.

The guiding calculation for our curve is then:

p(n+1) = p(n) + (curve_direction * perturb() *(1-t))

Here's an example rendering using the above principle:

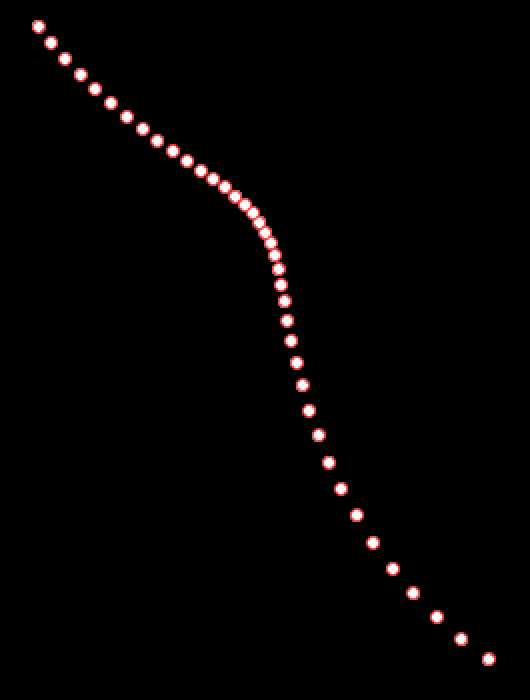
Filling Out The Curve

Observation: tentacles are thinner towards the ends.

Now we have a 1D curve, we can give it a 2nd dimension: thickness. Given a starting thickness_start and ending thickness_end, we can choose a thickness at each point on the curve using t:

thickness = thickness_start + (thickness_end-thickness_start)*t

This is also known as linear interpolation or 'lerp' so we'll use the proper term:

thickness = lerp(thickness_start, thickness_end, t)

Our curve changes direction along its length so we have to calculate a 'sideways' direction at each point to draw the width of the tentacle accurately at each point.

First, we need the direction of the curve at a given point:

dir = p(n+1) - p(n)

The 3D cross product of our direction and a unit vector up along positive z gives us a sideways vector:

sideways(n+0.5) = P x up

Note: strictly speaking dir gives a direction halfway between p(n) and p(n+1).

We can now draw our tentacle with thickness by drawing 'bones' along the curve or drawing either side of the tentacle by connecting the ends of each bone:

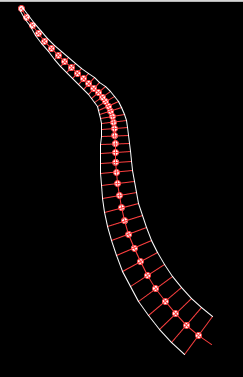
8 Tentacles Make A Cephalopod

Our simple direction model gives reasonable effects for a single curve. When we create a whole set of tentacles though, we want them all to share tentacleness but also to retain some individuality.

Considered from another angle, we want a generalised way to calculate curve direction at each point on each tentacle. We can create a function which provides direction value for each of our tentacles and whose value changes smoothly over the whole image.

Our direction function will use a set of 'attractor' points spread over the image, each with a defined radius of influence. The direction at a given position is the accumulated vector towards each point whose influence covers our sample position:

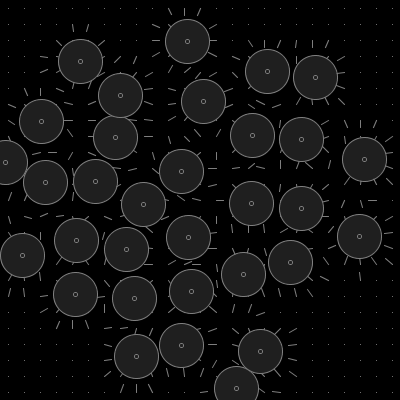
Observation: tentacles are more flexible towards the ends.

Now we can apply the direction function to our model in a realistic way by scaling its effect up towards the tentacle end:

p(n+1) = p(n) + (attractorFieldDirection(p(n)) * (1-t))

And finally, here's our final model in action:

Movement

What happens if we move our direction function's attractor points around?

What does that movement do to the tentacles?

Interesting.